In the last blog, I covered HyperLogLog (HLL) in Redis and spoke about how it can enable counting cardinalities of very large sets very efficiently. I concluded the blog by broadening the scope to counting the results of set operations. In this blog, I will expand on this scope.
To recap, some of the use cases of counting the results of set operations are as follows:
- Imagine we are maintaining Daily unique users in a set. Can I combine these sets to get weekly or monthly unique users? (akin to a rollup operation)
- Imagine I have a set of users who have visited a specific web page. And another who are from a particular locality. Can I combine these two sets to see which users from that locality visited the web page? (akin to a slice operation)
The first one is a set union operation and the second an intersection operation. These are the two basic operations we can expect to perform given two sets. So, how does HLL fare with these?
Unions in HLL
Unions are said to be ‘loss-less’ in HLL. In other words, they work extremely well. So, to get the count of the union of two sets, we can ‘merge’ the HLL data structures representing the two sets to get a new HLL data structure and get the count of the result. The merge operation for two HLLs with equal number of buckets involves taking the maximum value of each pair of buckets and assigning that as the value of the same bucket in the resultant HLL.
To see the intuition behind this, remember that the HLL algorithm only maintains the maximum number of consecutive zeros seen in the hashes of the items for a given bucket. So, if two items are hashing to the same bucket, the one with the maximum number of zeros contributes the value to be stored in the bucket. Hence, our algorithm for merging HLLs described above will be equivalent to replaying the stream by merging the original items.
In Redis, there is explicit support for this operation using a command called PFMERGE
- PFMERGE <result> <key1> <key2> … – Merges the HLLs stored at key1, key2, etc into result.
One can issue PFCOUNT <result> to get the cardinality of the union.
Some interesting points about unions:
- The merge operation is associative – hence we can merge multiple keys together into one single result, as indeed the PFMERGE command allows in Redis.
- The merge operation is parallelizable with respect to the buckets and hence can be implemented very fast.
- The merge operation assumes that the number of buckets is fixed between the sets being merged. When sizes are different, there is a way to ‘fold’ the HLL data structures with larger number of buckets into a HLL with the smallest number of buckets. This is described well here. I suppose the scenario of different bucket sizes arises if we are using some library where we could create a HLL with a specified bucket size. Of course, this is not applicable for Redis.
Intersections in HLL
Intersections in HLL are not loss-less. Again seeking into our intuitive explanation for unions, imagine we replay a merged set where only common items in 2 sets are included. If we add the distinct elements of the sets into this HLL, it is easy to see that the value of a bucket could be masked by a larger distinct value present in either of the original sets.
One possible way to workaround this limitation is to explore if it will be ok to maintain another key to just manage the intersection. For example, to satisfy the use case above, we could maintain one HLL for users who visited the web page, say users:<page>, and another for users from every locality, like users:<page>:<locality>. A stream processing framework will update both keys for an incoming event.
The good parts about this approach are:
- Number of updates will be bounded by the number of combinations of dimensions we want to count for. This can be done in a streaming manner for a small number of combinations.
- Reads of intersection counts will be fast and accurate too.
The issues with this approach are:
- It is easy to see that this can become a combinatorial nightmare with many different combinations of dimensions to maintain.
- Each intersection key would be more storage space, and hence causes more load, particularly for in-memory systems like Redis.
- The method would only work if all the dimensional information came in the same event. For e.g. if we got information about users visiting pages from one source and user-locality information from another, there would no way of updating the intersection key in a straightforward manner without doing a join.
Intersection using the Inclusion / Exclusion Principle
This is yet another approach talked about for computing intersections with HLLs. Dig into the set algebra, Venn diagrams and other such topics in your child’s math textbooks and you’ll find the Inclusion/Exclusion principle there. It just says:
| A u B | = | A | + | B | – | A n B | – where | A | means cardinality of set A.
So, can we say | A n B | = HLL(A) + HLL(B) – HLL(AuB)?
Folks at Neustar conducted experiments on this method and were kind enough to publish the results in a very detailed blog post. Again, recommended reading – for understanding how to frame an experiment for answering such a question.
To paraphrase the results, they defined two measures of sets:
- overlap(A, B) = | A n B | / | B |, where B is the smaller set.
- cardinality_ratio(A, B) = | A | / | B |, where B is the smaller set.
Using these measures, they formulated some empirical rules that determine when this method gave somewhat acceptable results. The results are within a reasonable error range when:
- overlap(A, B) >= overlap_cutoff, AND
- cardinality_ratio(A, B) < cardinality_ratio_cutoff
If one of these conditions is violated, they found the error % of the intersection could be high in the order of thousands. In their results, the cutoffs are given based on the bucket size. For the Redis bucket size (16384), this becomes:
- overlap(A, B) >= 0.05
- cardinality_ratio(A, B) < 20
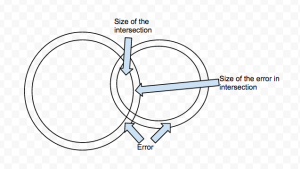
I reasoned the intuition behind these results from this diagram based off the Neustar blog (hopefully, I am not too far off):
A high error value of | A n B | results from both the sets contributing to the error almost equally or one of them dominating. In the case where both sets contribute the error almost equally, this can happen if the true value of intersection itself is very small compared to the size of the sets – measured by the overlap factor. In the cases where one of the sets contributes largely to the error, this can happen when the other set is very small compared to the size of the larger set – measured by the cardinality ratio.
Cases like these can certainly happen in real world. For e.g. our own use case of people who have visited a web page can be very large compared to the people who live in a certain locality – if the locality is very small.
So, to summarise, using the Inclusion / Exclusion principle allows us to compute an estimate for the intersection cardinality with no additional state or storage. It can also be done reasonably fast due to the low latency of APIs like PFCOUNT and PFMERGE. However, for certain commonly occurring use cases, its error ratios are likely to be unusably large.
In the next post, I will explore an alternative approach to intersections using a different sketching algorithm that is said to provide better results. I will also discuss results of my own tests comparing the accuracy of the two algorithms.
Excellent post (as well as the one before) – waiting to learn more about HLL intersections!
Thank you, @itamarhaber! Will post the last one in a couple of days, or early next week.